Notebooks

Cuadernos de Álgebra Lineal

Los cuadernos de Álgebra Lineal abarcan tanto temas fundamentales como aplicaciones prácticas. Comienzan con una introducción a las matrices, donde se muestra su estructura y se explican las operaciones básicas. También incluyen un estudio detallado de los vectores, resaltando su representación en Julia y las operaciones básicas asociadas.

Además de estos conceptos básicos, los cuadernos contienen aplicaciones prácticas como el procesamiento de imágenes, donde se utiliza el álgebra lineal para manipular píxeles y aplicar filtros y kernels. También se exploran temas como la descripción de grafos mediante matrices, el clustering en machine learning y la independencia lineal de vectores y matrices.

Los cuadernos abordan temas avanzados como la diagonalización de matrices, ilustrando su aplicación a la sucesión de Fibonacci. También se cubre la compresión de imágenes mediante la descomposición en valores singulares (SVD) y técnicas de marca de agua digital. Además, se incluyen temas como el análisis de componentes principales (PCA), sistemas de ecuaciones diferenciales, mínimos cuadrados y ajuste polinomial.

Cuadernos de Análisis Numérico

Los cuadernos de Análisis Numérico comienzan mostrando la representación de números enteros y de punto flotante, mostrando cómo los errores de redondeo y los límites de precisión afectan los cálculos numéricos. También incluyen una introducción al cálculo simbólico con la librería Symbolics.

En temas de comparación asintótica, se definen conceptos como el orden asintótico para sucesiones y se utilizan ejemplos gráficos para ilustrar la convergencia. Se abordan la convergencia lineal, superlineal y la expansión de Taylor para la aproximación de funciones.

Los métodos numéricos para encontrar raíces de funciones, como bisección, Newton y punto fijo, son explorados con implementaciones prácticas en el cuaderno Ecuaciones No Lineales. También se discuten ecuaciones lineales, incluyendo la factorización LU y de Cholesky, con ejemplos en Julia.

El cuaderno sobre Círculos de Gershgorin presenta métodos para localizar valores propios de matrices, extendiendo la teoría a discos de Brauer y discos generalizados de Gershgorin.

La interpolación se aborda mediante polinomios y splines, mostrando cómo garantizar la suavidad en los puntos de unión y aplicaciones en datos caligráficos. El ajuste de curvas incluye enfoques como el ajuste lineal y polinómico cúbico, aplicados al crecimiento de tumores en ratones.

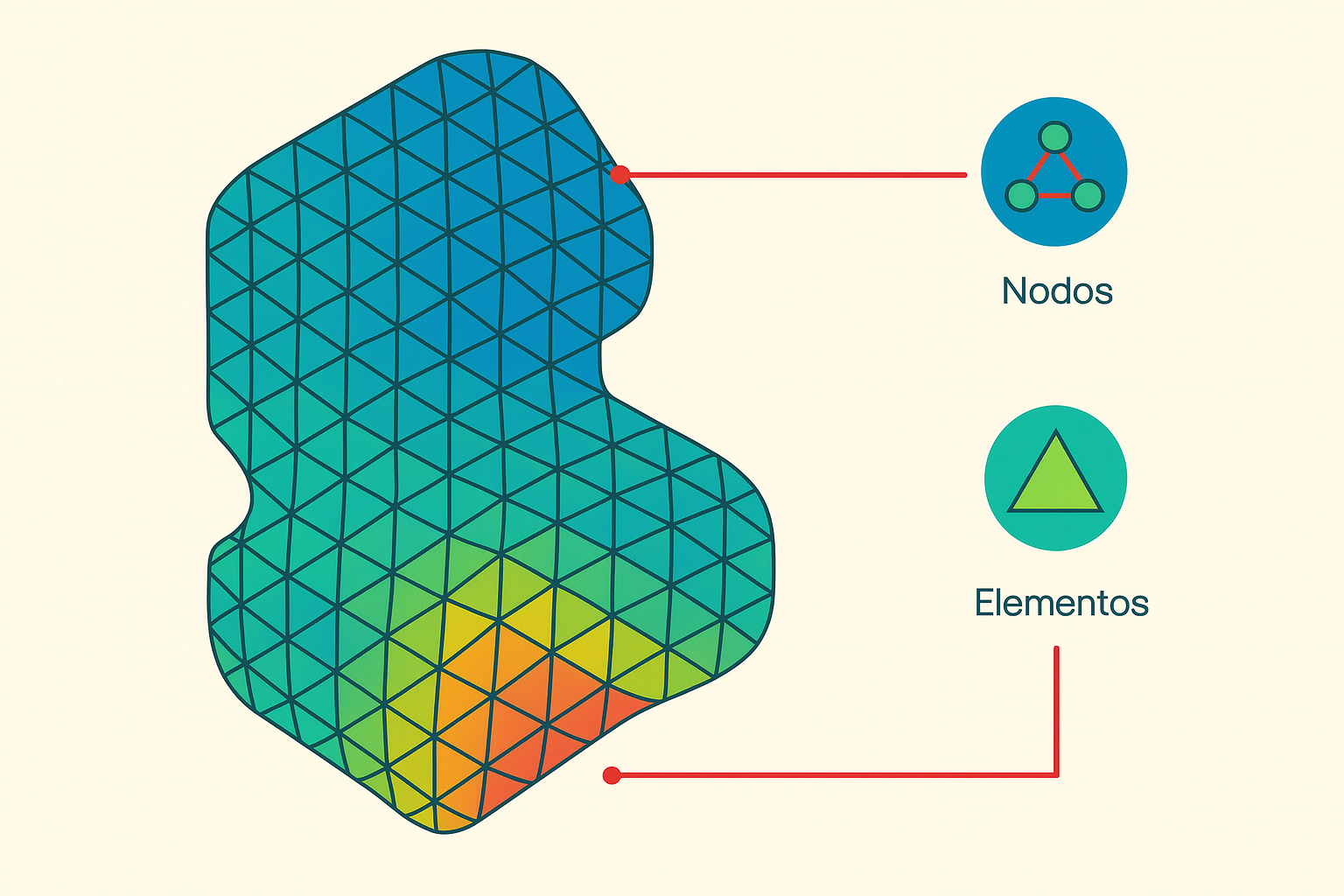
Finalmente, los métodos de integración numérica como las sumas de Riemann, la regla del trapecio y la regla de Simpson se ilustran con ejemplos prácticos. El método de elementos finitos se utiliza para resolver ecuaciones como la de Poisson, aplicando discretización y condiciones de frontera en dominios unidimensionales y bidimensionales.

Cuadernos sobre Ecuaciones Diferenciales Ordinarias

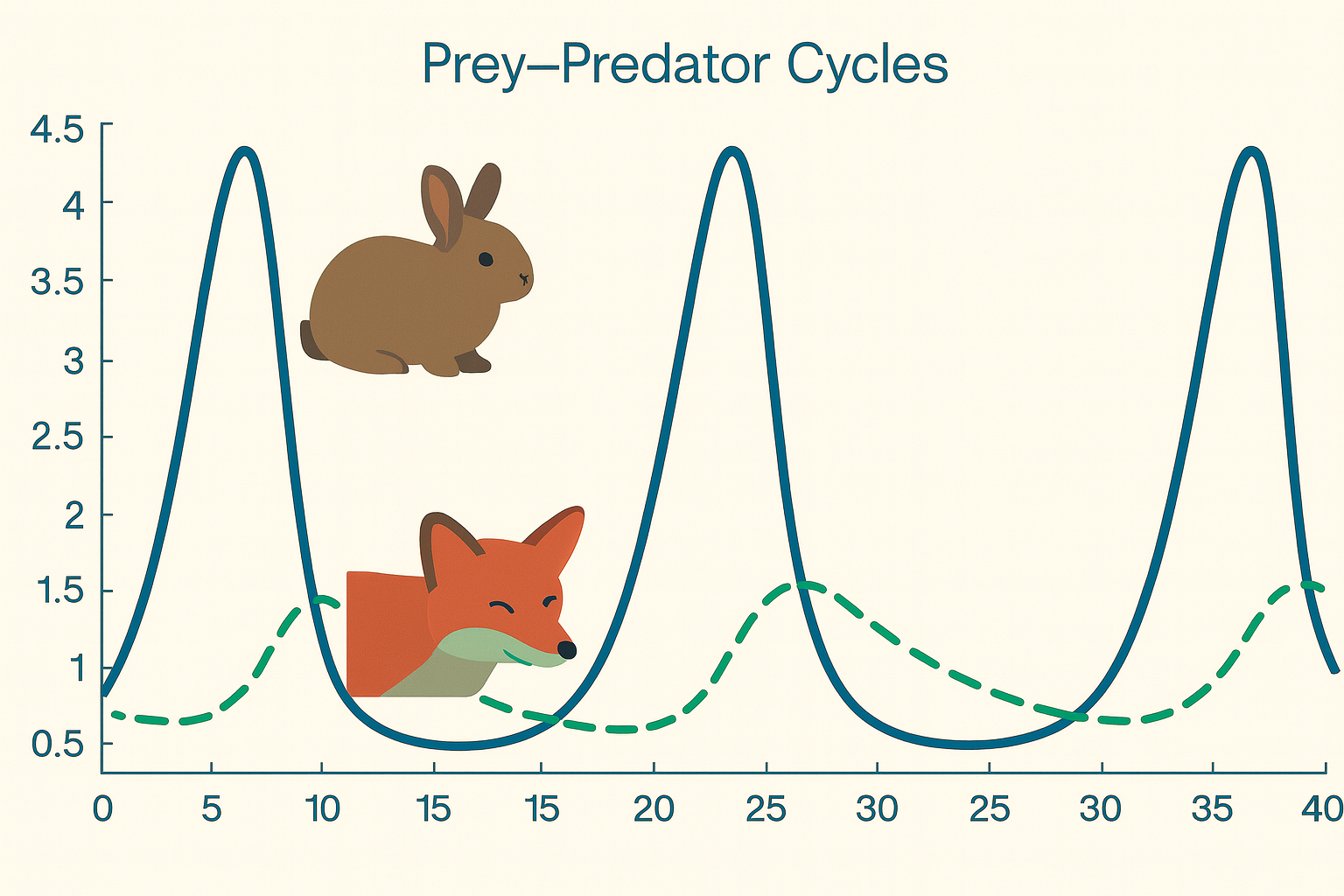
Los cuadernos sobre ecuaciones diferenciales ordinarias abarcan una amplia gama de temas matemáticos y prácticos. Desde la introducción a la modelación matemática y las ecuaciones diferenciales hasta la resolución de problemas específicos como el crecimiento de poblaciones, el movimiento de planetas o la dosificación de medicamentos, estos cuadernos ofrecen un panorama completo de cómo las ecuaciones diferenciales se aplican en diferentes contextos.

Además, exploran técnicas numéricas y analíticas para resolver ecuaciones, ajustar modelos a datos experimentales y comprender fenómenos naturales y sociales.

Introducción a las Ciencias de la Computación y la Programación

Los cuadernos sobre el curso Introducción a las Ciencias de la Computación y la Programación están en construcción.

Cuadernos sobre Optimización

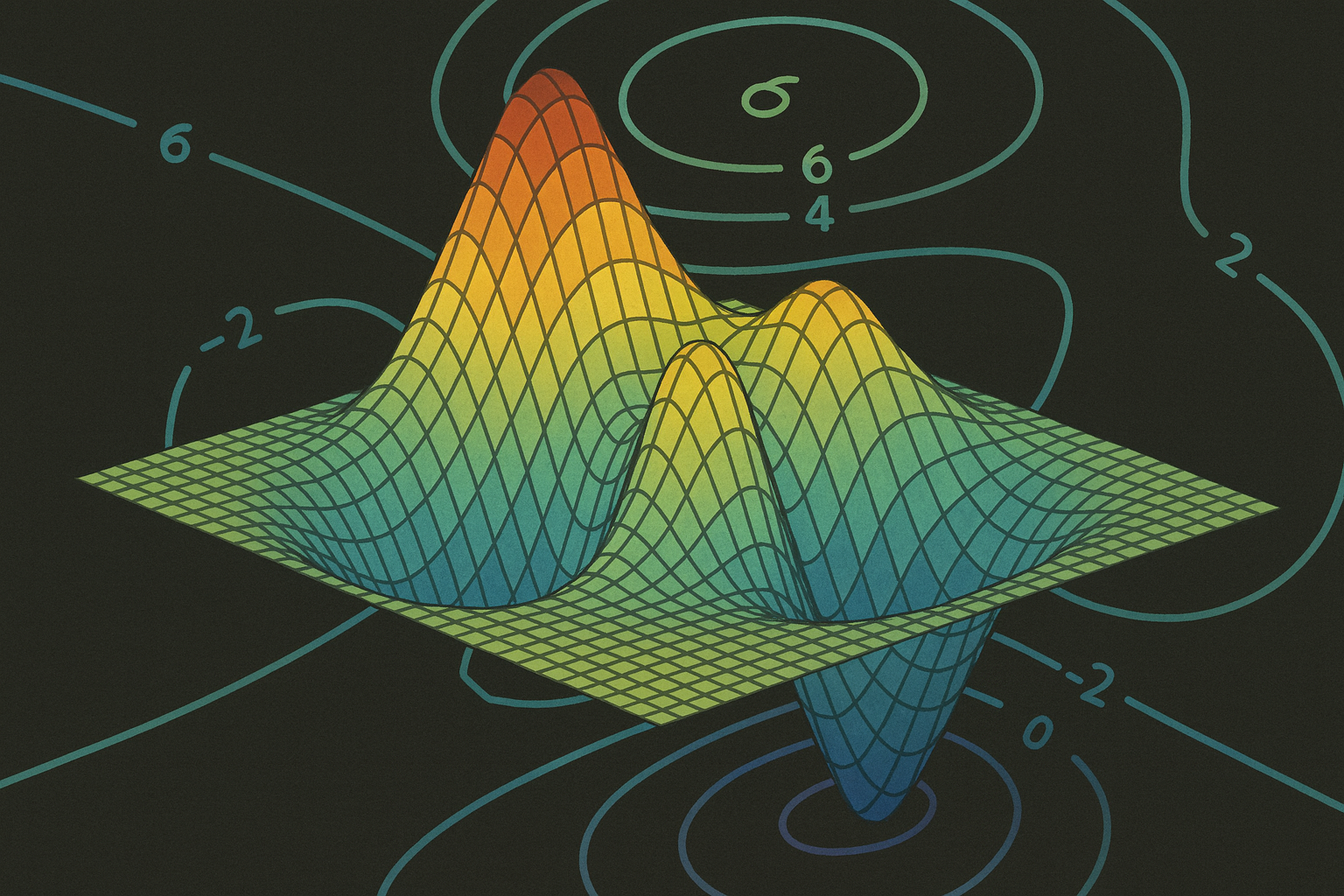
Los cuadernos sobre optimización muestran temas clave en la mejora de decisiones y procesos. En el problema de la dieta, se busca la combinación óptima de alimentos para satisfacer requisitos nutricionales a bajo costo, influenciados por el problema de Stigler, con implicaciones de seguridad alimentaria. El cuaderno de métodos de descenso explora técnicas de optimización numérica, incluyendo el descenso de gradiente y el método de Newton, con aplicaciones prácticas y visualizaciones para facilitar la comprensión.

Cuadernos sobre Variable Compleja

Los cuadernos sobre variable compleja se enfocan en diversos temas. Desde la introducción a la representación y operaciones básicas con números complejos hasta la visualización de funciones complejas y la exploración de conjuntos de Julia utilizando técnicas iterativas y de graficación en el plano complejo, estos cuadernos ofrecen un completo panorama de cómo se estudian y aplican los conceptos de variable compleja en Julia.