Álgebra Lineal

Introducción a las Matrices

En este notebook, se presenta una introducción a las matrices. Se explica que una matriz es un conjunto rectangular de números, símbolos o expresiones organizados en filas y columnas, representados con letras mayúsculas y con su dimensión indicada por el número de filas y columnas.

Se muestran ejemplos de matrices reales, simbólicas y de números complejos, junto con la explicación detallada de cómo acceder a elementos específicos y mostrar submatrices. Se introducen conceptos como matrices menores y por bloques, con ejemplos prácticos.

Se exploran tipos de matrices como cuadradas, diagonales, identidad y nulas, con ejemplos aleatorios y operaciones básicas como suma y multiplicación por escalar. Se abordan operaciones más avanzadas, como la multiplicación de matrices por vectores, entre matrices y el producto de Kronecker, con ejemplos prácticos utilizando matrices aleatorias.

Introducción a los Vectores

El cuaderno comienza explicando los vectores como conjuntos ordenados de números, resaltando su representación en Julia mediante el tipo de dato Array. Se exploran operaciones básicas, como la dimensión del arreglo.

Se detalla el acceso a elementos, introduciendo el uso de índices y la función end. Se muestra cómo trabajar con subconjuntos de vectores mediante rangos, la comparación de vectores y de elementos individuales.

Se introducen vectores nulos, canónicos y de unos, mostrando cómo construir manualmente vectores canónicos en Julia. Se utiliza el paquete Plots.jl para generar gráficos de vectores y visualizar datos.

Las operaciones con vectores se abordan desde la suma componente a componente hasta la multiplicación y división por escalares, proporcionando ejemplos prácticos.

Introducción al procesamiento de imágenes

Este notebook introduce el procesamiento de imágenes mediante representaciones numéricas de intensidad y los canales RGB. Se destaca la creación interactiva del notebook en Pluto.jl, usando librerías como Colors e ImageShow.

La exploración de píxeles y matrices revela propiedades RGB y facilita la manipulación eficiente de imágenes. Se abordan operaciones como la selección de subimágenes, el ajuste de tamaños y el uso del operador de Broadcasting para manipulación de datos.

Finalmente, se presentan operaciones avanzadas de procesamiento como la reducción de tamaño y la inversión, utilizando álgebra lineal para reescalar píxeles y realizar combinaciones lineales.

Para concluir, el notebook muestra la aplicación de filtros y kernels, ilustrando cómo estos pueden ser utilizados en diferentes operaciones de procesamiento de imágenes.

Descripción de grafos usando matrices

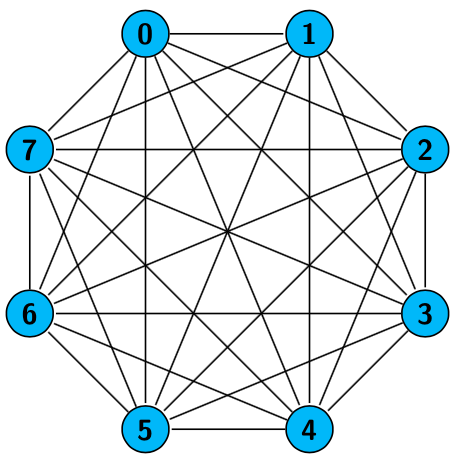
Este cuaderno introduce conceptos básicos de grafos, como nodos, aristas y adyacencia, ilustrados mediante el famoso problema de los Puentes de Königsberg.

Se explican los distintos tipos de nodos y aristas, destacando cómo la flexibilidad de los grafos permite representar diversas estructuras. A través de ejemplos interactivos, se construyen y visualizan grafos usando la librería GraphPlot.

También se introducen las matrices de adyacencia e incidencia, utilizadas para representar conexiones entre nodos y aristas, facilitando el análisis y comprensión de las estructuras de grafos.

Finalmente, se presentan generadores de grafos incorporados, permitiendo crear grafos con diferentes características para fines de estudio y experimentación.

Clustering

El cuaderno comienza con una introducción al machine learning, destacando la importancia de la distancia euclidiana en el contexto del clustering.

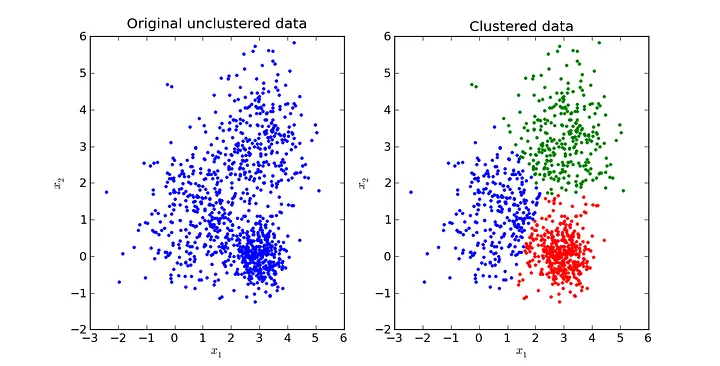
Se presenta una función para evaluar la calidad de los clusters y se introduce el algoritmo K-Means, con una implementación y un ejemplo de aplicación a datos generados aleatoriamente.

Además, se aborda el preprocesamiento de datos, que incluye la carga desde archivos y la generación aleatoria de datos.

Se detallan técnicas de normalización y estandarización, proporcionando funciones para Min-Máx y Z-Score.

La visualización de datos antes y después de la normalización se presenta, seguida de la aplicación del algoritmo K-Means y la visualización de los clusters resultantes.

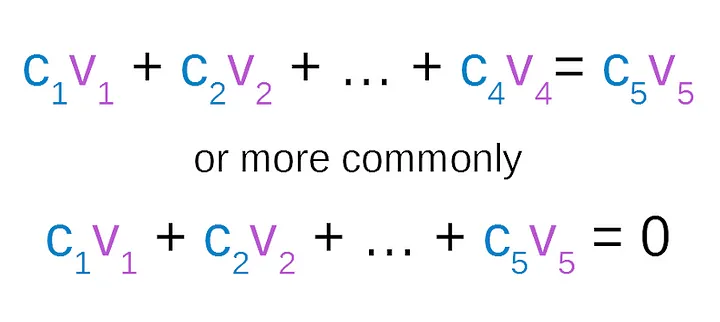
Independencia Lineal I

El cuaderno comienza introduciendo el concepto de independencia lineal. Se define la dependencia e independencia lineal, relacionándolos con la existencia de combinaciones lineales no triviales.

Se muestra un teorema clave que establece la relación de dependencia lineal entre dos vectores cuando uno es un múltiplo escalar del otro, ilustrando este concepto con un ejemplo específico.

Luego, se explora la relación entre matrices y la independencia lineal, destacando que las columnas de una matriz son linealmente independientes si y solo si el determinante de la matriz es diferente de cero.

Se proporcionan ejemplos adicionales para determinar la dependencia o independencia lineal de conjuntos de vectores en \(\mathbb{R}^n\), utilizando el concepto de determinante para tomar decisiones sobre la independencia lineal.

Se introduce el concepto de base en un espacio vectorial, demostrando que cualquier conjunto de \(n\) vectores linealmente independientes en \(\mathbb{R}^n\) genera todo el espacio, ilustrado con un ejemplo específico.

El cuaderno concluye abordando el tema de vectores ortonormales y presenta el proceso de ortogonalización de Gram-Schmidt para convertir un conjunto linealmente independiente en un conjunto ortonormal.

Se describen las variantes clásica y modificada del algoritmo de Gram-Schmidt, y se demuestra su aplicación en un ejemplo práctico, proporcionando código para implementar estos algoritmos.

Independencia Lineal II

Este notebook presenta una introducción a la factorización QR, un método clave para descomponer una matriz \( A \) en el producto de una matriz ortogonal \( Q \) y una matriz triangular superior \( R \).

La descomposición QR se utiliza para resolver sistemas de ecuaciones lineales y problemas de optimización. El cuaderno describe métodos para obtener la factorización QR, centrándose en las reflexiones de Householder y las rotaciones de Givens.

Primero, se explican las propiedades y el cálculo de las matrices de Householder, que se utilizan para transformar un vector en un múltiplo de un vector canónico, facilitando la ortogonalización de las columnas de una matriz. Se proporciona un algoritmo para calcular el vector y el coeficiente de Householder, junto con ejemplos prácticos.

Luego, se muestra cómo usar las reflexiones de Householder para triangularizar una matriz y obtener la matriz \( R \), así como la matriz \( Q \) mediante acumulación progresiva. Finalmente, se introducen las rotaciones de Givens, que son especialmente útiles para matrices dispersas, mostrando cómo aplicar estas rotaciones para lograr una factorización QR eficiente.

Diagonalización (Sucesión de Fibonacci)

El cuaderno comienza con la importación de librerías. Luego, aborda el tema de matrices semejantes, proporcionando definiciones y ejemplos. También incluye un teorema que establece que matrices semejantes tienen el mismo polinomio característico y, por lo tanto, los mismos valores propios.

Se presentan ejemplos de matrices semejantes y se verifica que comparten los valores propios. Luego, se introduce el concepto de matriz diagonalizable, junto con un teorema que establece las condiciones para que una matriz sea diagonalizable. Se presenta un corolario que afirma que si una matriz tiene valores propios distintos, entonces es diagonalizable.

Se proporcionan ejemplos de matrices diagonalizables y se calculan sus valores y vectores propios. Posteriormente, se explora la aplicación de estos conceptos a la sucesión de Fibonacci. Se describe cómo se puede expresar el sistema recursivo de Fibonacci en términos matriciales y se muestra cómo calcular directamente el n-ésimo número de Fibonacci mediante la diagonalización de la matriz asociada.

Se implementa una función para calcular \(F_n\) de manera eficiente utilizando la diagonalización.

Compresión de imágenes (SVD)

En este cuaderno, se presentan definiciones de valor y vector propio. Posteriormente, se muestra cómo hallar los valores singulares de una matriz. A continuación, se detalla la descomposición en valores singulares (SVD) con diversos ejemplos.

Luego, nos enfocamos en la descomposición en valores singulares reducida, que es la que utiliza Julia, y se muestran ejemplos específicos. Después de explorar la SVD, se muestra la compresión de imágenes. Este proceso implica realizar la SVD de la imagen y luego truncar dicha descomposición en \(k\) valores singulares (se realiza esto en cada canal de color para luego ensamblar nuevamente la imagen).

Con este concepto presente, se presenta la creación de una marca de agua digital. Esta técnica permite personalizar imágenes sin que sea perceptible al ojo humano. La marca de agua se inserta creando una perturbación en la matriz \(V\). Una vez que la imagen está marcada, se muestra cómo deducir y recuperar la marca de agua.

Análisis de componentes principales (PCA)

Este cuaderno aborda el Método de Análisis de Componentes Principales (PCA), una técnica de reducción de dimensionalidad. Comienza explicando conceptos como la media y la varianza en un conjunto de datos.

Luego, se presenta la covarianza y la matriz de covarianza, seguidas por el proceso detallado de cómo se emplea el PCA. Se describen los pasos desde la centralización de datos y cálculo de la matriz de covarianza hasta la reconstrucción de datos y la compresión de imágenes utilizando las componentes principales.

Se muestra cómo la compresión efectiva mantiene la información esencial de la imagen original mientras reduce su dimensionalidad. Además, se incluyen ejemplos prácticos de compresión de imágenes con diferentes números de componentes principales y se evalúa el error de compresión en cada caso.

Sistemas de ecuaciones diferenciales

Se comienza con una introducción sobre ecuaciones diferenciales, destacando la forma general de las ecuaciones de primer orden y proporcionando un ejemplo específico. Luego, presentan una solución numérica para el ejemplo utilizando la biblioteca DifferentialEquations de Julia.

El cuaderno continúa con una sección sobre sistemas lineales homogéneos. Se introduce la notación matricial y se explica cómo resolver sistemas lineales homogéneos mediante el uso de matrices diagonalizables. Se presenta un ejemplo concreto, mostrando cómo la solución general de un sistema homogéneo se puede expresar en términos de los vectores propios y valores propios de la matriz asociada al sistema. Luego, se muestra cómo resolver un sistema específico con condiciones iniciales dadas.

Círculos de Gershgorin

Este cuaderno muestra los métodos de localización de valores propios, comenzando con el Teorema de Gershgorin, que establece que todos los valores propios de una matriz están contenidos en la unión de discos en el plano complejo. Luego, se extiende la teoría a los discos de Brauer y a los discos generalizados de Gershgorin, mostrando mejoras en las estimaciones sobre la ubicación de los valores propios.

Además, se proporciona una serie de ejemplos prácticos que ilustran la aplicación de estos teoremas y métodos, mostrando cómo se pueden visualizar los discos correspondientes para diferentes matrices y cómo estos métodos pueden ser utilizados en la práctica para análisis y simulaciones.

Mínimos cuadrados

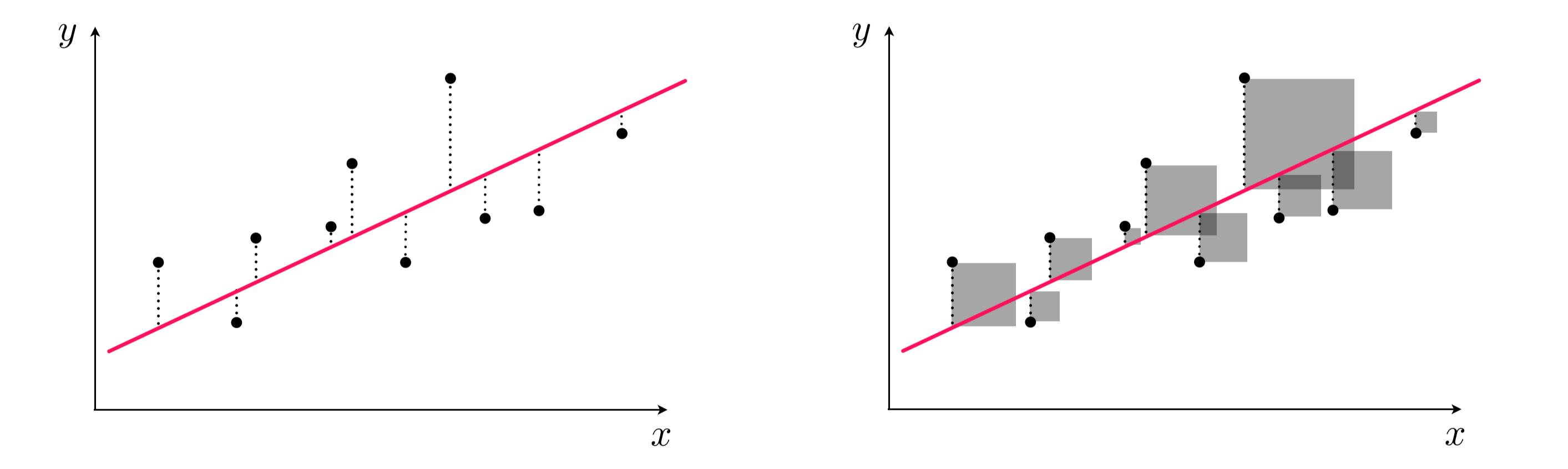
El cuaderno proporciona una introducción al método de mínimos cuadrados, destacando su aplicación para resolver sistemas sobredeterminados de ecuaciones lineales. Luego, se presenta un ejemplo con datos y se resuelve utilizando el operador de backslash (\) en Julia.

Posteriormente, el cuaderno aborda el ajuste por mínimos cuadrados en el contexto de la regresión lineal y presenta un ejemplo específico de ajuste polinomial. Se describe cómo se puede aplicar el método para encontrar un polinomio de grado específico que se ajuste de manera óptima a un conjunto de datos dado.

Finalmente, se explora el ajuste por mínimos cuadrados de ecuaciones cuadráticas en las variables x e y, y se proporciona un ejemplo práctico con datos que se ajustan a una elipse.