Análisis Numérico

Enteros y Punto Flotante

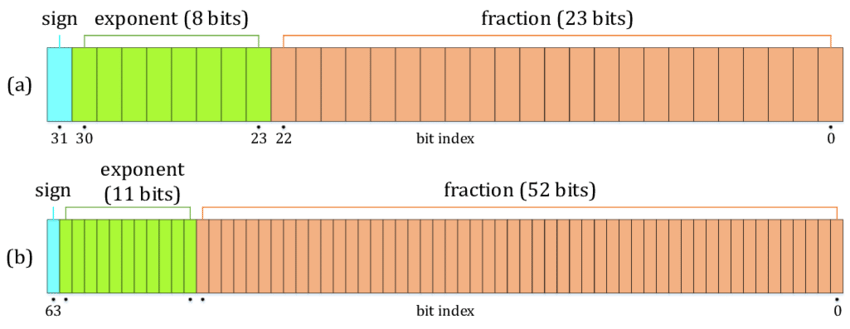
Este cuaderno muestra la representación de números enteros y de punto flotante. Comienza mostrando cómo se representan los enteros utilizando bits, proporcionando ejemplos prácticos y conversiones de enteros a cadenas de bits.

Luego, se muestran los números de punto flotante, explicando su representación detallada, incluyendo el signo, el exponente y el significando, y cómo estas representaciones pueden afectar los cálculos numéricos debido a errores de redondeo y límites de precisión.

También se muestra una introducción al cálculo simbólico utilizando la librería Symbolics, mostrando cómo realizar operaciones simbólicas que no dependen de valores numéricos específicos.

Comparación asintótica

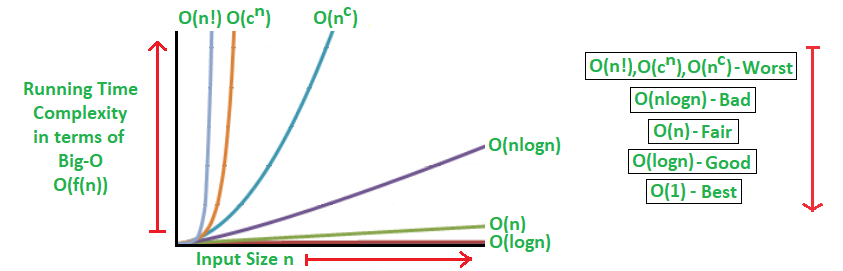
El cuaderno comienza definiendo los conceptos de orden asintótico para sucesiones, como \(x_n = \mathcal{O}(\alpha_n)\) y \(x_n = \mathcal{o}(\alpha_n)\), que indican cómo las sucesiones \(x_n\) y \(\alpha_n\) convergen hacia cero en comparación. Proporciona ejemplos gráficos para ilustrar estas comparaciones, como \(\frac{n+1}{n^2}\) en relación con \(\frac{1}{n}\), y \(\frac{1}{n \log(n)}\) también en relación con \(\frac{1}{n}\), entre otros.

El cuaderno también explora la velocidad de convergencia, describiendo la convergencia lineal y superlineal con ejemplos como \(x_n = 0.5^n\) y \(x_n = 0.5^{n^2}\). Además, aborda la convergencia de orden y cómo se puede demostrar mediante gráficos, como el caso de \(x_n = 0.5^{2^n}\).

Finalmente, se introduce la expansión de Taylor, explicando cómo aproximar funciones mediante polinomios de Taylor y su error asociado. El cuaderno utiliza la librería TaylorSeries para generar y trabajar con estos polinomios.

Ecuaciones No Lineales

El cuaderno trata sobre métodos numéricos para encontrar las raíces de una función real \( f: \mathbb{R} \to \mathbb{R} \). Se exploran varios métodos, incluyendo el de bisección, el de Newton y el método del punto fijo.

El método de bisección se basa en la propiedad de cambio de signo de la función en un intervalo y se implementa para encontrar raíces de funciones continuas. El método de Newton utiliza la derivada para iterar hacia una raíz, y el método de punto fijo busca un valor \( x^* \) tal que \( F(x^*) = x^* \).

El cuaderno también presenta implementaciones y ejemplos prácticos usando la función \( \exp(x) - \sin(x) \) para ilustrar cada método.

Ecuaciones No Lineales II

Este cuaderno aborda tres métodos para resolver ecuaciones no lineales y diferenciales: Newton, Euler y Picard.

El Método de Newton aproxima raíces de funciones no lineales, Euler resuelve ecuaciones diferenciales ordinarias con variantes explícita e implícita, y Picard utiliza aproximaciones iterativas basadas en integrales para garantizar la convergencia.

Ecuaciones Lineales

El cuaderno comienza con una introducción al sistema de ecuaciones lineales representado por la ecuación \( A x = b,\) donde \( A \) es una matriz y \( x \) y \( b \) son vectores. Luego, explora cómo calcular diferentes normas de vectores y matrices en Julia, proporcionando ejemplos prácticos de cómo obtener normas subordinadas y de Frobenius.

Luego, se presenta la factorización LU, incluyendo un algoritmo para descomponer una matriz en productos de matrices triangulares y cómo implementarlo en Julia. Se presentan ejemplos de factorización LU con matrices específicas, incluyendo la verificación de la precisión de la factorización mediante normas. También se discute la factorización PA=LU con pivoteo, utilizando ejemplos adicionales como la matriz de Hilbert y matrices diagonales dominantes. Luego de esto, el cuaderno aborda la factorización de Cholesky para matrices simétricas y definidas positivas, y cómo resolver sistemas lineales en Julia usando el operador backslash.

Interpolación

El cuaderno muestra, primero el problema de encontrar un polinomio de menor grado que pase por un conjunto de puntos dados \((x_i, y_i)\), es decir, la interpolación polinomial, y se describen las formas de Newton y Lagrange para calcular este polinomio.

Además, se explora la interpolación por splines, que utiliza polinomios de grado \(k\) en intervalos distintos, garantizando suavidad en las derivadas de orden \(k-1\) en los puntos de unión. Se muestran ejemplos de la aplicación de splines constantes, lineales y cúbicos en datos caligráficos.

Ajuste de Curvas

El cuaderno aborda el ajuste de curvas y datos, explorando métodos para encontrar modelos que describan con precisión el comportamiento de datos observados, centrándose en el crecimiento de tumores en ratones.

Se discuten varios enfoques, como el ajuste lineal, polinómico cúbico, redes neuronales artificiales y ecuaciones diferenciales, específicamente el modelo de Von Bertalanffy. El ajuste de curvas busca establecer relaciones entre variables optimizando los parámetros del modelo para minimizar el desajuste entre datos observados y generados, utilizando la técnica de mínimos cuadrados basada en la norma euclidiana.

Integración Numérica I

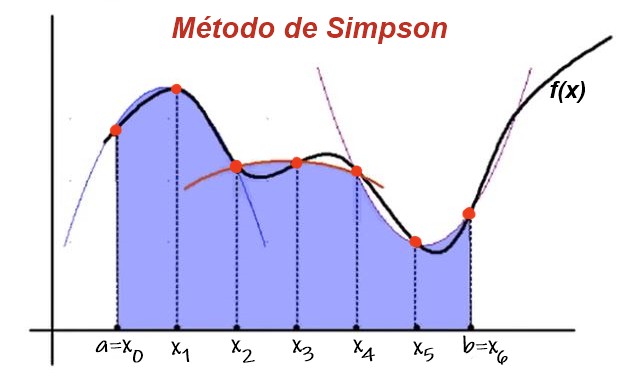
En este cuaderno se estudian métodos de integración numérica como las sumas de Riemann, la regla del trapecio y la regla de Simpson.

Estos métodos dividen un intervalo \([a,b]\) en subintervalos y aproximan el área bajo una curva utilizando rectángulos o trapecios. Se ejemplifica con las funciones \(y=x^2\) en \([0,3]\) y \(y=e^{x^2}\) en \([0,1]\), mostrando cómo estas técnicas convergen hacia el área exacta conforme se aumenta el número de subintervalos. Estos métodos son esenciales para calcular áreas bajo curvas cuando la función no tiene una integral elemental.

Método de Elementos Finitos

Este cuaderno se centra en el método de elementos finitos. En primer lugar, se estudia el comportamiento de la cuerda elástica en una dimensión.

Aquí, discretizamos el dominio y resolvemos ecuaciones lineales con condiciones de frontera específicas. Observamos cómo los resultados varían según ajustamos los parámetros del problema. En la segunda parte, se muestra como resolver la ecuación de Poisson de manera numérica en un dominio bidimensional usando elementos finitos, esto con la ayuda de la librería Gridap.