Procesamiento de Imágenes

El cuaderno aborda conceptos básicos y aplicaciones del procesamiento de imágenes digitales en escala de grises y a color. Introduce formatos como RGB, CMY y YCbCr, y analiza cómo las imágenes pueden representarse como matrices de valores de píxeles. Además, explora cómo manipular imágenes mediante ajustes de brillo, contrastes y operaciones matemáticas en matrices.
Se presentan ejemplos prácticos, como la visualización y modificación de imágenes en escala de grises, y la construcción de objetos geométricos, desde figuras simples hasta fractales como el triángulo de Sierpinski. También se explica la importancia del análisis estadístico de imágenes mediante histogramas para evaluar características como brillo y contraste.

Se presentan métricas con referencia completa, como el Error Cuadrático Medio (MSE) y la Relación Señal-Ruido de Pico (PSNR), que comparan imágenes procesadas con una referencia ideal para cuantificar la distorsión. Además, se analizan métricas sin referencia, como el Índice de Similitud Estructural (SSIM) y su extensión Multi-SSIM, que evalúan la calidad visual considerando luminancia, contraste y estructura sin necesidad de una imagen ideal. También se discute el error estructural y su relación con estas métricas, proporcionando ejemplos numéricos y cálculos aplicados a imágenes de prueba.

Se abordan aplicaciones de funciones elementales en el procesamiento de imágenes digitales, centrándose en transformaciones potenciales, exponenciales y logarítmicas para mejorar la iluminación y el contraste. Presenta técnicas como la corrección gamma, que ajusta el brillo de imágenes mal expuestas mediante funciones de potencia. También incluye herramientas para transformar imágenes entre espacios de color RGB y YCbCr, aplicando correcciones específicas en el canal de luminancia (Y). Además, se implementan funciones para visualizar histogramas y ajustar niveles de brillo y contraste. El cuaderno utiliza imágenes subexpuestas y sobreexpuestas como ejemplos, mostrando sus respectivas transformaciones y resultados.

Este cuaderno aborda el procesamiento de imágenes mediante transformaciones lineales y técnicas de automatización para mejorar la calidad visual. Se presentan funciones auxiliares en Julia para realizar tareas como la conversión entre espacios de color RGB y YCbCr, ajuste de valores de píxeles, creación de histogramas y transformaciones específicas para mejorar el contraste. Se introduce la trasformación lineal como una herramienta para expandir el rango de valores de los píxeles y mejorar significativamente el contraste de las imágenes. Además, se describe una variación de esta técnica que utiliza transformaciones lineales a trozos para ajustar los percentiles de los píxeles a intervalos uniformemente distribuidos. El cuaderno incluye ejemplos visuales que muestran los efectos de estas transformaciones.
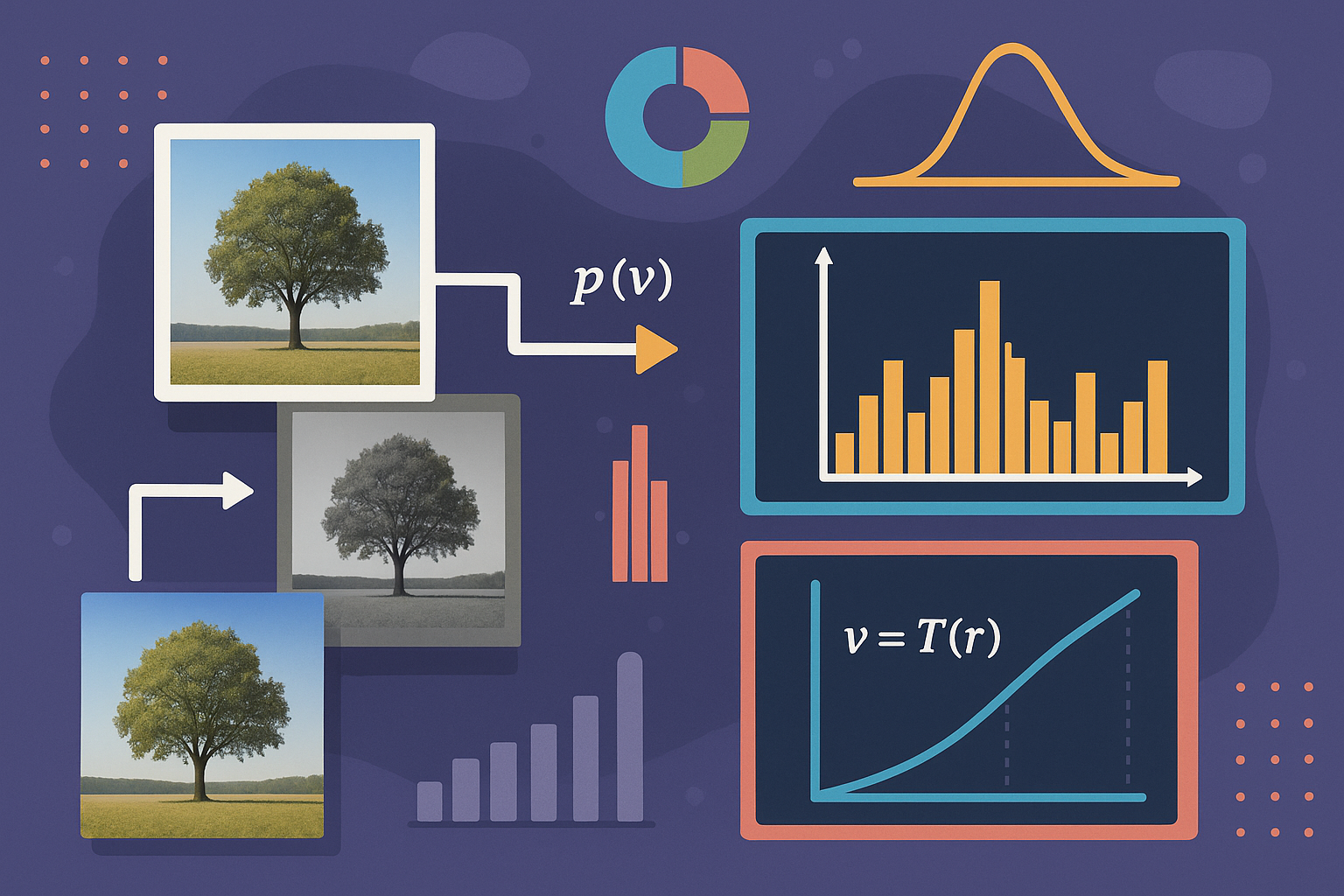
Se define la relación entre imágenes digitales y variables aleatorias, donde cada píxel representa un valor que puede ser modelado como una variable aleatoria con una distribución de probabilidad. Se detalla cómo los histogramas de las imágenes representan gráficamente estas distribuciones, y cómo pueden transformarse para cumplir ciertos objetivos mediante técnicas como la ecualización del histograma. Este procedimiento busca lograr distribuciones uniformes, garantizando que todos los tonos de gris estén representados equitativamente. Además, el cuaderno introduce el teorema de transformación de variables aleatorias, explicando cómo modificar una variable aleatoria con una función de densidad conocida para que adopte otra distribución deseada.
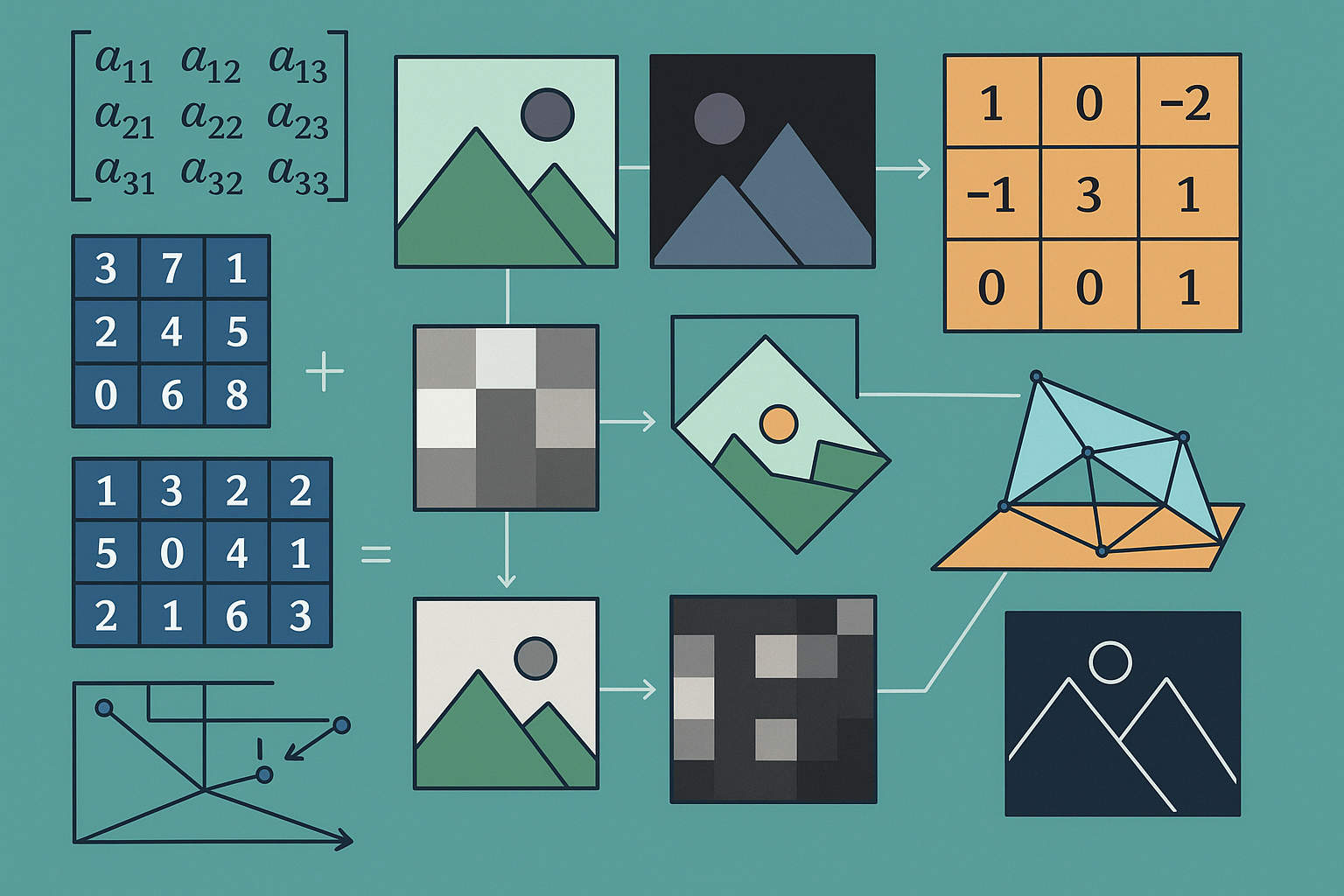
El cuaderno explora cómo las matrices y las transformaciones lineales pueden aplicarse en el procesamiento de imágenes. El contenido incluye operaciones básicas con matrices, como la generación del negativo de una imagen, la transposición para rotaciones y reflejos, la sobreposición mediante la suma de matrices, y el producto de matrices para efectos como compresión y resaltado de bordes. También se describen métodos para segmentar partes específicas de imágenes usando matrices personalizadas. Se muestra también como modificar imágenes mediante rotaciones y cambios de perspectiva utilizando coordenadas homogéneas y proyectivas.
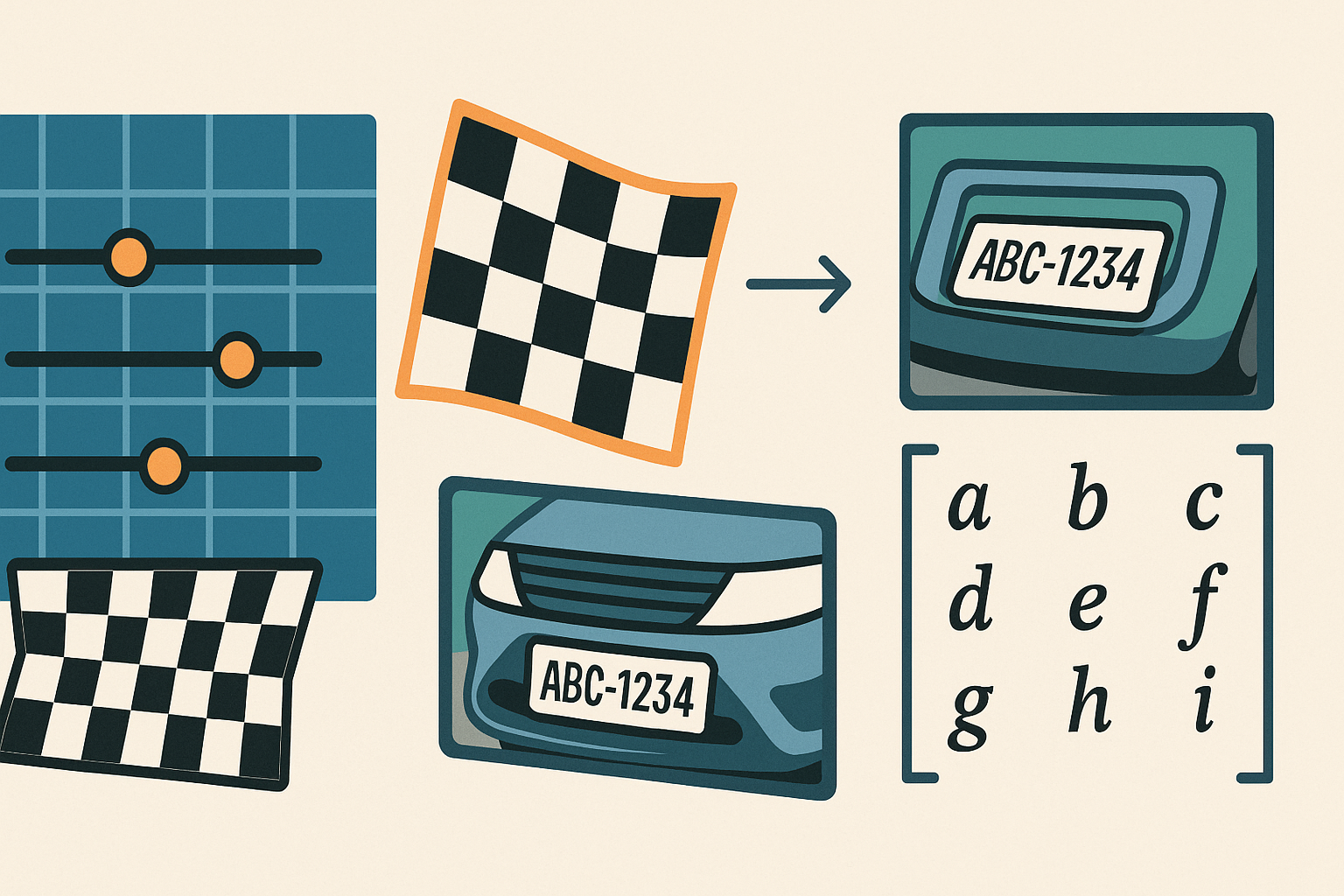
El cuaderno explora el uso de coordenadas homogéneas y transformaciones proyectivas para modelar y aplicar homografías en imágenes mediante Julia y PlutoUI: primero presenta una demo interactiva con sliders para ajustar en tiempo real los parámetros de la matriz 3 × 3 (rotación, escala, traslación y perspectiva) sobre una imagen de prueba con cuadros; luego describe cómo, dados cuatro pares de puntos correspondientes (por ejemplo, los vértices de una placa vehicular), se arma y resuelve un sistema lineal homogéneo para obtener la matriz de homografía usando espacios nulos, y se aplica píxel a píxel la transformación para rectificar la perspectiva de una imagen real.
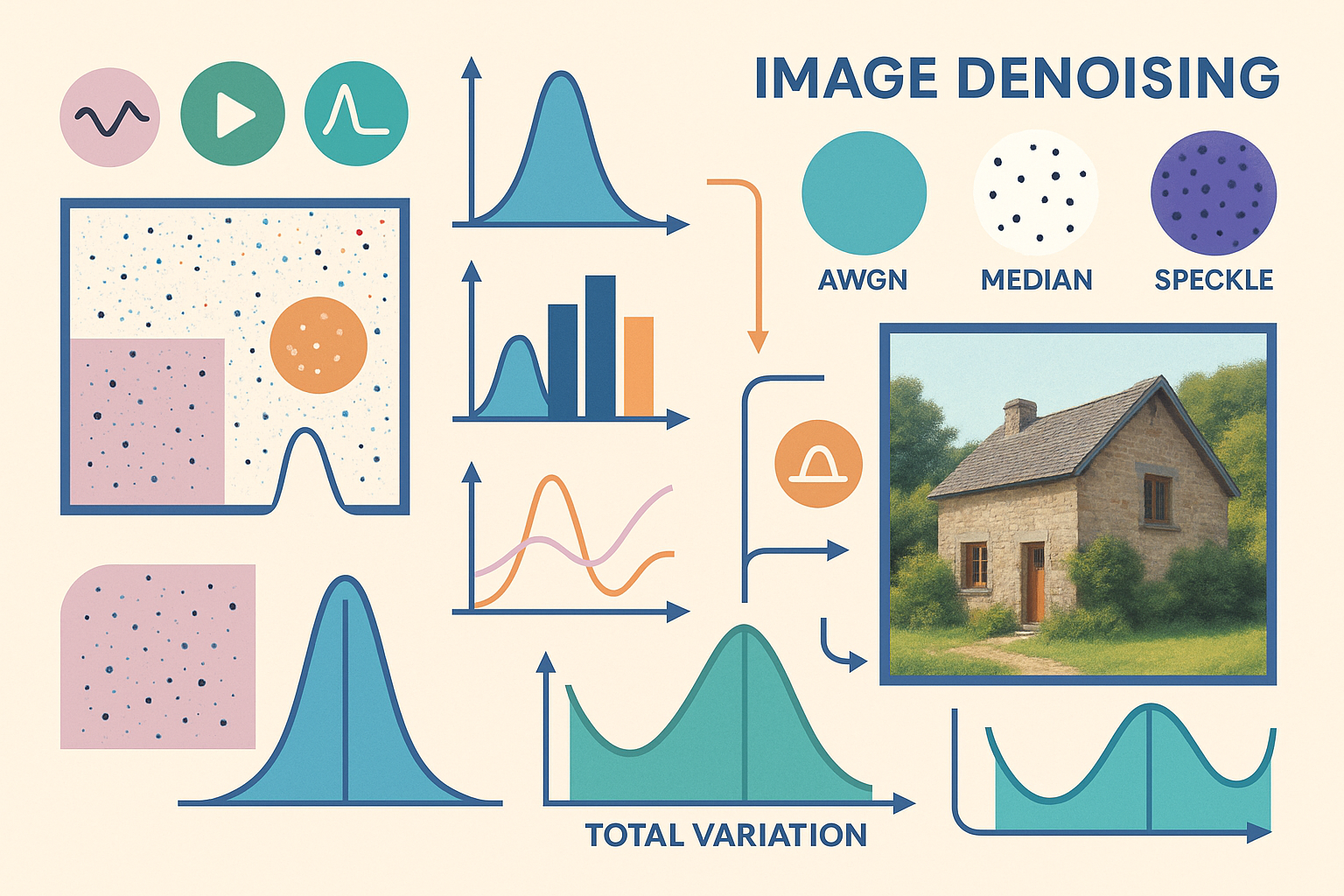
El cuaderno explora técnicas de restauración de imágenes afectadas por ruido. Aborda tres tipos de ruido: AWGN (variaciones aleatorias normales), sal y pimienta (píxeles dispersos blancos y negros) y speckle (ruido multiplicativo típico en imágenes médicas). Se muestran métodos de difuminado, como el promedio simple, gaussiano y convolución, que suavizan imágenes reduciendo ruido. También se explican técnicas de filtrado como el filtrado de mediana, efectivo contra el ruido sal y pimienta, y el filtrado por variación total, que equilibra reducción de ruido y preservación de detalles. Cada método es evaluado en imágenes con diferentes tipos de ruido, destacando sus fortalezas según el caso. Incluye referencias útiles y es una guía práctica para aprender y aplicar procesamiento de imágenes.
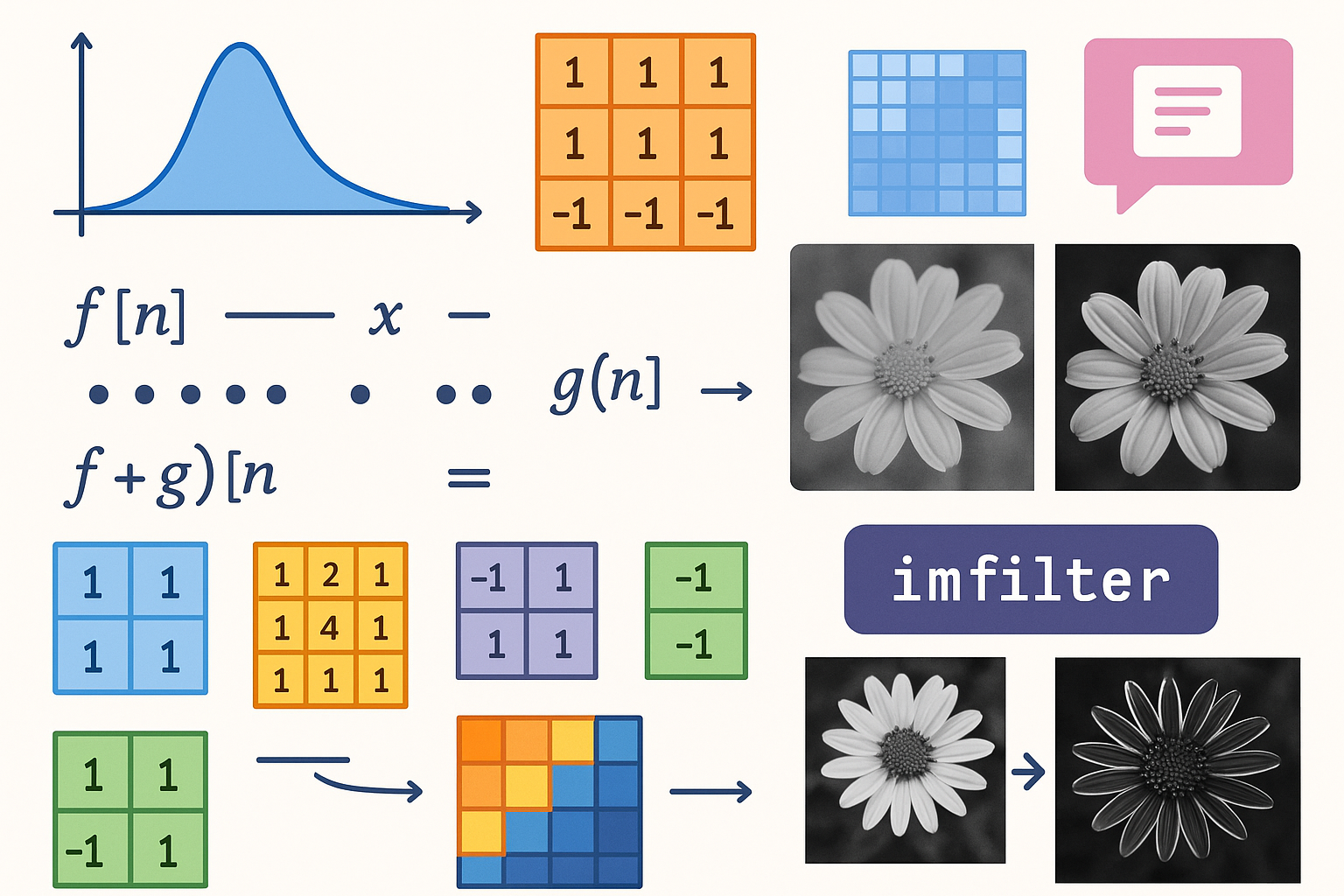
Este cuaderno trata sobre el uso de la convolución y el filtrado de imágenes. Se inicia con una introducción a diferentes variantes de convoluciones (continuas, discretas, lineales, circulares, entre otras) y se centra en las convoluciones lineales y circulares, tanto para secuencias como para matrices. Posteriormente, se muestra cómo se aplica la convolución en el procesamiento de imágenes. Esto incluye el uso de kernels (también llamados filtros) que permiten realizar transformaciones locales, como suavizado, detección de bordes y mejora de detalles en imágenes. Ejemplos prácticos muestran cómo utilizar la convolución para modificar matrices asociadas a imágenes y obtener efectos específicos. Además, se exploran diferentes tipos de kernels y sus aplicaciones. Entre ellos se incluyen filtros de identidad, detección de bordes, realce, desenfoque y gradientes, con ejemplos que ilustran cómo aplicarlos mediante la función imfilter.
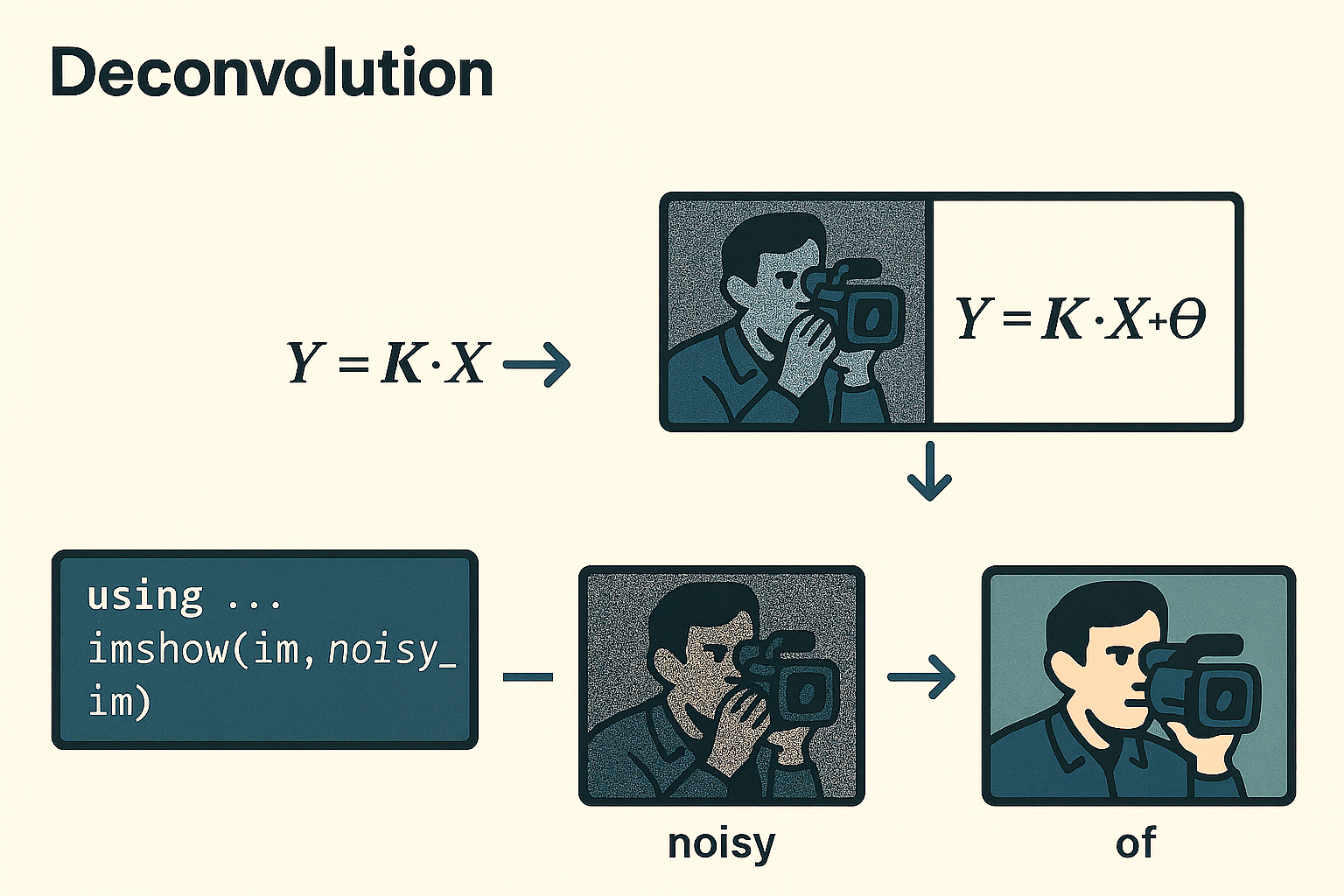
El cuaderno presenta la deconvolución como un problema inverso de restauración de imágenes degradadas por desenfoque y ruido: parte de un ejemplo con la imagen “camarógrafo” distorsionada mediante un kernel separable K = u vT y contaminada con ruido gaussiano, luego muestra cómo modelar la convolución como una transformación lineal Y = K * X + Θ usando matrices de convolución y vectorización/Kronecker para obtener vec(Y) = MK vec(X) + θ. A continuación, explica la inversión directa mediante la descomposición en valores singulares de MK y demuestra sus limitaciones (valores singulares cercanos a cero), para luego implementar y comparar dos estrategias de regularización, Tikhonov y TSVD, mostrando sus fórmulas, código en Julia y resultados gráficos de recuperación con y sin ruido. Finalmente incluye referencias clave para profundizar en problemas inversos y deconvolución.
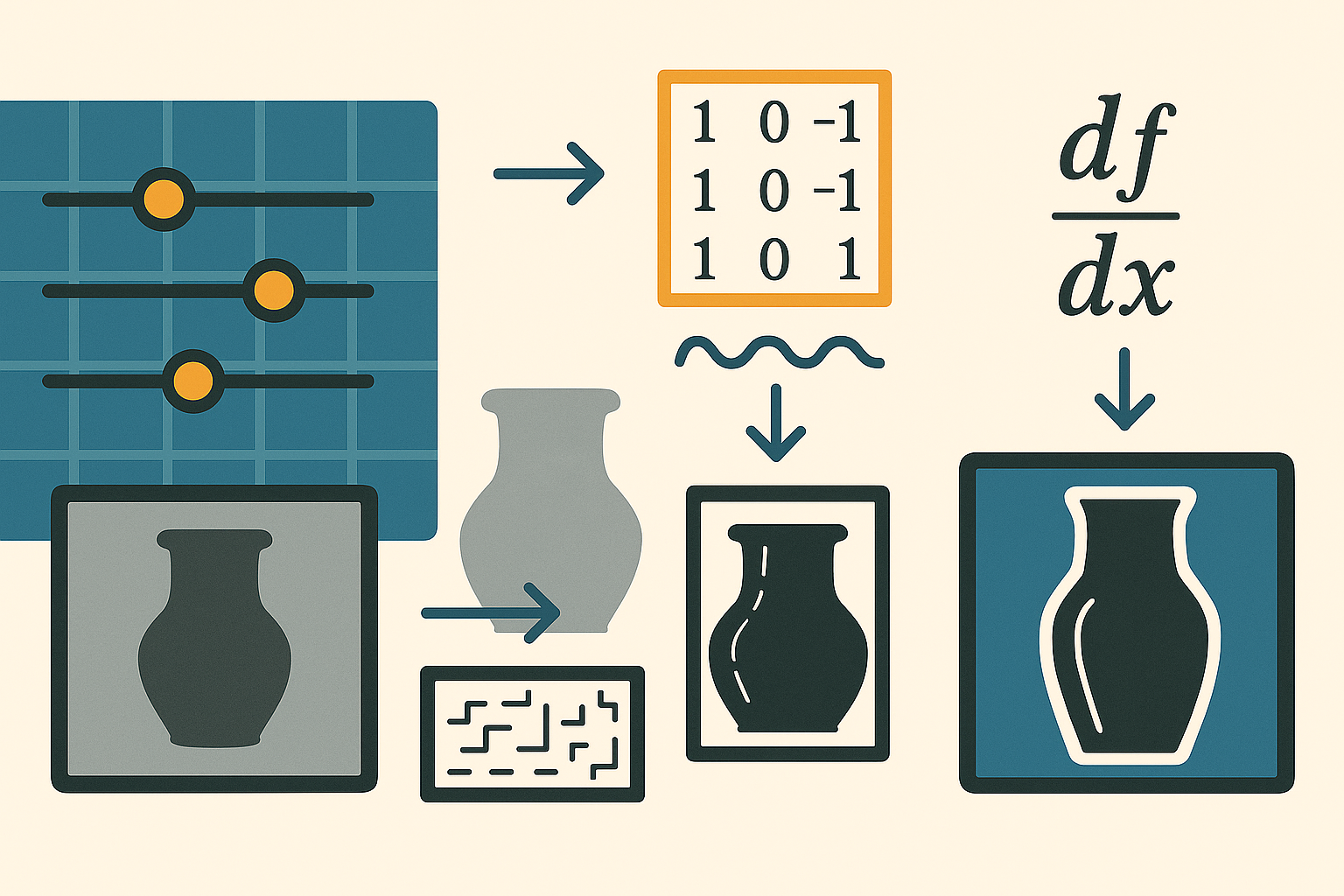
El cuaderno comienza con el método del gradiente, que calcula diferencias horizontales y verticales para estimar la magnitud y dirección del cambio de intensidad; sigue con el operador cruzado de Roberts, sensible a bordes diagonales a ±45°, luego desarrolla el método de Prewitt, que amplía la vecindad considerada para robustecer la detección, y el método de Sobel, que pondera más los píxeles contiguos; a continuación propone el detector laplaciano, que emplea una sola convolución con un kernel centrado en la segunda derivada discreta; analiza cómo el ruido gaussiano degrada estos detectores y sugiere prefiltrar con un filtro gaussiano o con la Laplaciana de Gaussiana para mejorar la resistencia al ruido; finalmente muestra cómo, tras binarizar el resultado de un detector (por ejemplo Sobel), aplicar convolución booleana y dilatación con distintos elementos estructurales ensancha y refina los bordes obtenidos.
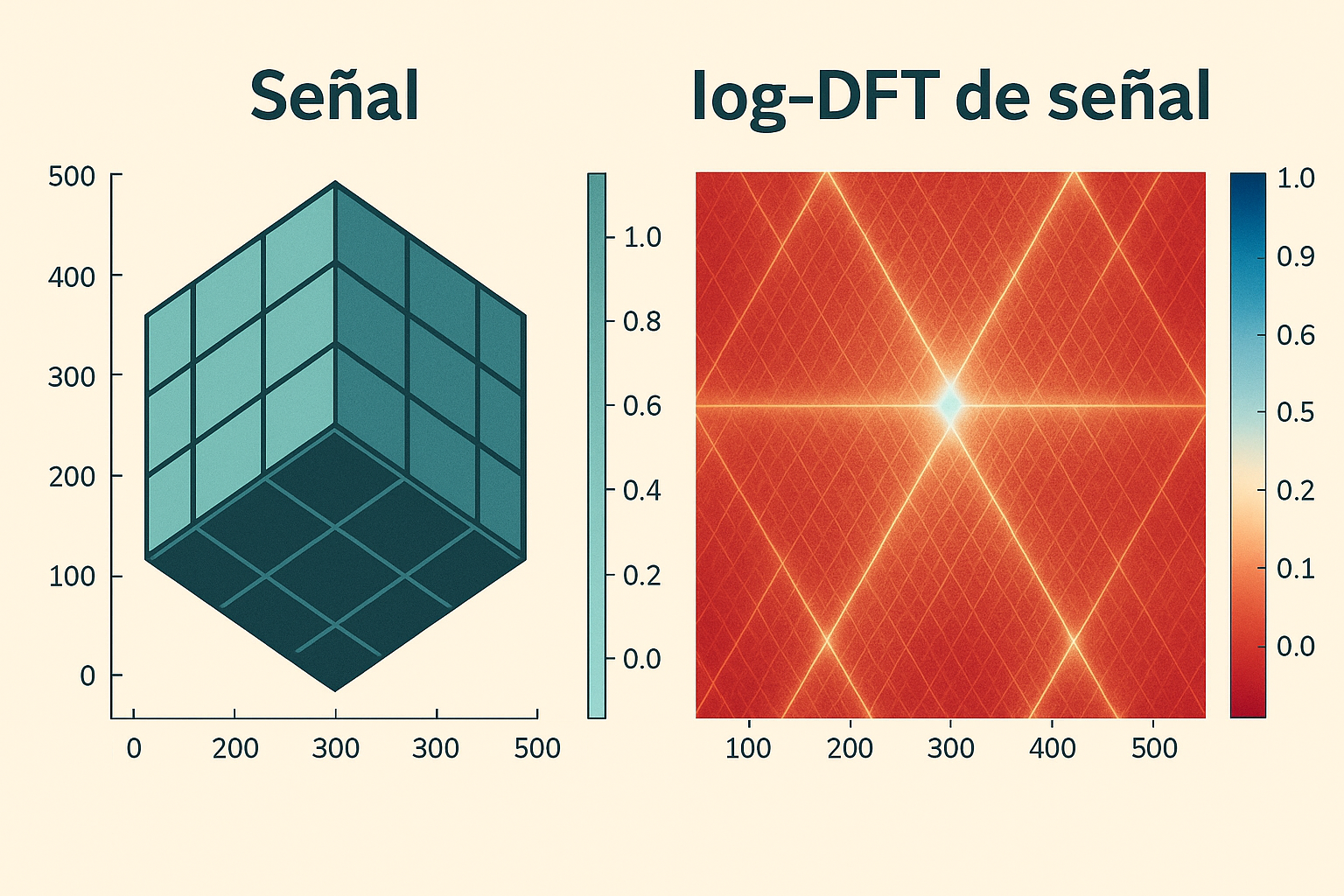
El cuaderno introduce la Transformada Discreta de Fourier (DFT) como herramienta fundamental para analizar y procesar señales e imágenes en el dominio de la frecuencia. En una dimensión define la DFT y su inversa, muestra propiedades de periodicidad y simetría de secuencias sinusoidales, presenta la representación matricial y explica cómo usar la función fft de Julia para descomponer señales, graficar magnitudes y fases con fftshift y aplicar escalado logarítmico para mejorar la visualización. A continuación expande la teoría a dos dimensiones con la 2-D DFT y su inversa, ilustra teoremas de multiplicación y de convolución circular en el plano bidimensional y ejemplifica con patrones espaciales simples. En la sección de filtrado muestra cómo aplicar filtros ideales de paso bajo y paso alto, filtros gaussianos y la técnica optimizada “Laplaciana de Gaussiana” en el dominio de la frecuencia mediante controles interactivos en Pluto. Finalmente presenta la relación entre la transformada de la respuesta al impulso (PSF u OTF) y la restauración de imágenes degradadas por convolución, y cierra con referencias clave.
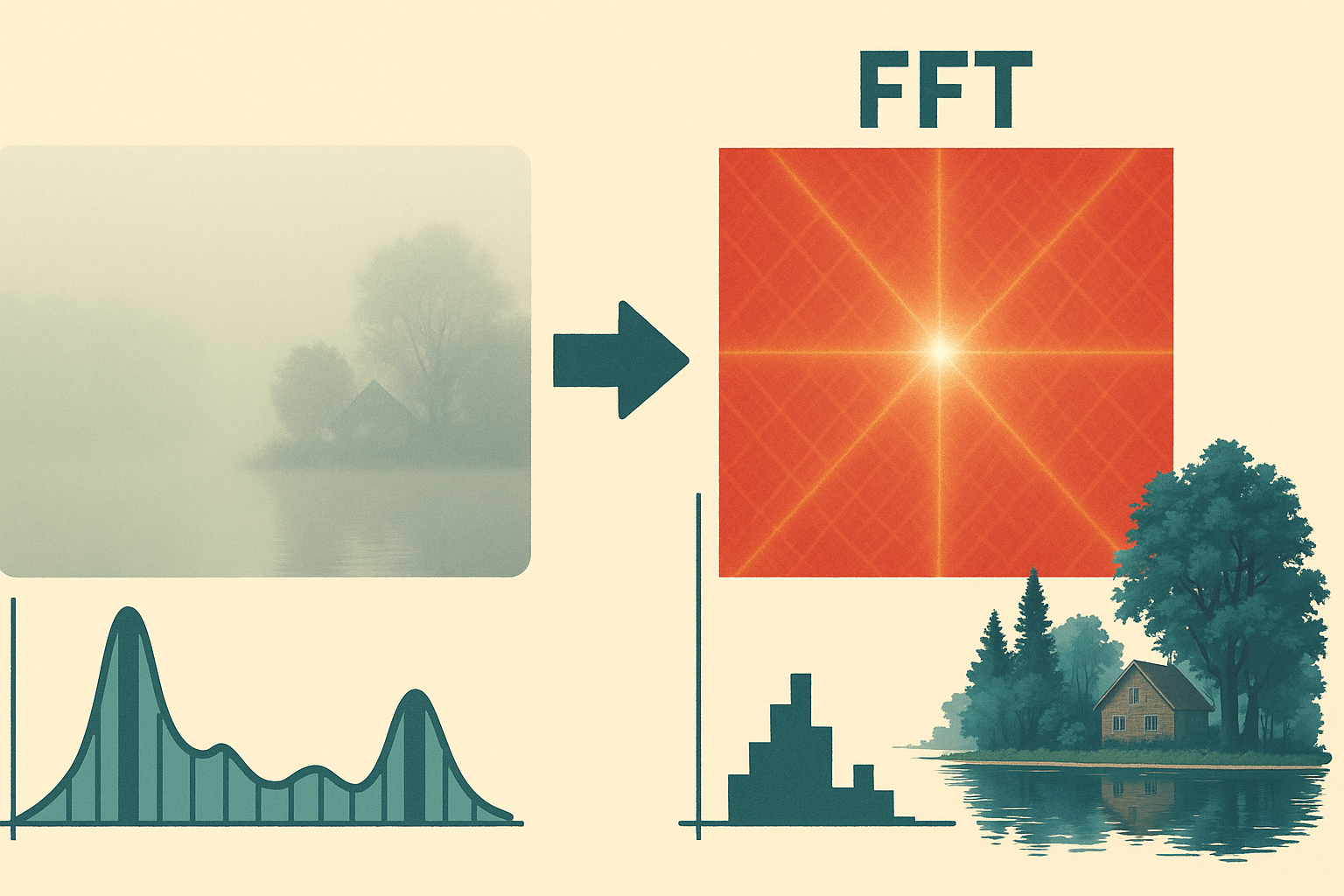
El cuaderno desarrolla un estudio aplicado de la Transformada de Fourier en el procesamiento y restauración de imágenes con neblina, basado en el modelo atmosférico de dispersión y en el método de Roy–Chaudhuri. Se presenta el modelo físico que describe la imagen observada como una combinación entre la imagen original y la luz atmosférica, y se explica cómo estimar la transmisión luminosa mediante el canal oscuro y la luz del aire. Posteriormente, se aplica una regularización en el dominio de Fourier usando la Transformada Rápida de Fourier (FFT) para eliminar componentes de baja frecuencia responsables del blanqueamiento y mejorar el contraste sin alterar los colores. El proceso se complementa con un ajuste de contraste basado en el índice de Michelson para optimizar la percepción visual.